Model Selection¶
In Bayesian statistics, an objective model comparison is carried out by comparing the models’ marginal likelihood. The likelihood function describes the probability (density) of the data, given the parameter values (and thereby the chosen model). By integrating out (marginalizing) the parameter values, one obtains the marginal likelihood (also called the model evidence), which directly measures the fitness of the model at hand. The model evidence represents a powerful tool for model selection, as it does not assume specific distributions (e.g. Student’s t-test assumes Gaussian distributed variables) and automatically follows the principle of Occam’s razor.
The forward-backward algorithm that bayesloop allows to approximate the model evidence based on the discretized parameter distributions. Details on this method in the context of Hidden Markov models can be found here.
This section aims at giving a very brief introduction of Bayes factors together with an example based on the coal mining data and further introduces combined transition models in bayesloop.
In [1]:
%matplotlib inline
import matplotlib.pyplot as plt # plotting
import seaborn as sns # nicer plots
sns.set_style('whitegrid') # plot styling
import numpy as np
import bayesloop as bl
# prepare study for coal mining data
S = bl.Study()
S.loadExampleData()
L = bl.om.Poisson('accident_rate', bl.oint(0, 6, 1000))
S.set(L)
+ Created new study.
+ Successfully imported example data.
+ Observation model: Poisson. Parameter(s): ['accident_rate']
Bayes factors¶
Instead of interpreting the value of the marginal likelihood for a single model, it is common to compare two competing models/explanations \(M_1\) and \(M_2\) by evaluating the Bayes factor, here denoted as \(B_{12}\). The Bayes factor is given by the ratio of the two marginal likelihood values:
where \(p(D|M_i)\) states the probability of the data (marginal likelihood) given model \(M_i\). A value of \(B_{12} > 1\) therefore indicates that the data is better explained by model \(M_1\), compared to \(M_2\). More detailed information for the interpretation of the value of Bayes factors can be found here and in the references therein.
As a first example, we investigate whether the inferred disaster rate of
the coal mining data set indeed should be modeled as a time-varying
parameter (a constant rate is an equally valid hypothesis). We first fit
the model using the GaussianRandomWalk transition model with a
standard deviation of \(\sigma = 0.2\) to determine the
corresponding model evidence (on a log scale). Subsequently, we use the
simpler Static transition model (assuming no change of the disaster
rate over time) and compare the resulting model evidence by computing
the Bayes factor. Note that for computational efficiency, the keyword
argument evidenceOnly=True is used, which evaluates the model
evidence, but does not store any results for plotting.
In [2]:
# dynamic disaster rate
T = bl.tm.GaussianRandomWalk('sigma', 0.2, target='accident_rate')
S.set(T)
S.fit(evidenceOnly=True)
dynamicLogEvidence = S.log10Evidence
#static disaster rate
T = bl.tm.Static()
S.set(T)
S.fit(evidenceOnly=True)
staticLogEvidence = S.log10Evidence
# determine Bayes factor
B = 10**(dynamicLogEvidence - staticLogEvidence)
print '\nBayes factor: B =', B
+ Transition model: Gaussian random walk. Hyper-Parameter(s): ['sigma']
+ Started new fit:
+ Formatted data.
+ Set prior (function): jeffreys. Values have been re-normalized.
+ Finished forward pass.
+ Log10-evidence: -74.59055
+ Transition model: Static/constant parameter values. Hyper-Parameter(s): []
+ Started new fit:
+ Formatted data.
+ Set prior (function): jeffreys. Values have been re-normalized.
+ Finished forward pass.
+ Log10-evidence: -88.00564
Bayes factor: B = 2.60066520417e+13
The computed Bayes factor \(B = 2.6 \cdot 10^{13}\) shows decisive support for the first hypothesis of a dynamic disaster rate.
While this analysis conducted above clearly rules for a time-varying
rate, there may still exist a dynamic model that represents a better fit
than the Gaussian random walk with \(\sigma=0.2\). A very simple
dynamic model is given by the transition model ChangePoint that
assumes an abrupt change of the disaster rate at a predefined point in
time, we choose 1890 here. Note that the transition model
ChangePoint does not need a target parameter, as it is applied
to all parameters of an observation model. We perform a full fit in this
case, as we want to provide a plot of the result.
In [3]:
# dynamic disaster rate (change-point model)
T = bl.tm.ChangePoint('tChange', 1890)
S.set(T)
S.fit()
dynamicLogEvidence2 = S.log10Evidence
# determine Bayes factor
B = 10**(dynamicLogEvidence2 - dynamicLogEvidence)
print '\nBayes factor: B =', B
plt.figure(figsize=(8, 4))
plt.bar(S.rawTimestamps, S.rawData, align='center', facecolor='r', alpha=.5)
S.plot('accident_rate')
plt.xlim([1851, 1962])
plt.xlabel('year');
+ Transition model: Change-point. Hyper-Parameter(s): ['tChange']
+ Started new fit:
+ Formatted data.
+ Set prior (function): jeffreys. Values have been re-normalized.
+ Finished forward pass.
+ Log10-evidence: -74.41178
+ Finished backward pass.
+ Computed mean parameter values.
Bayes factor: B = 1.50929883739
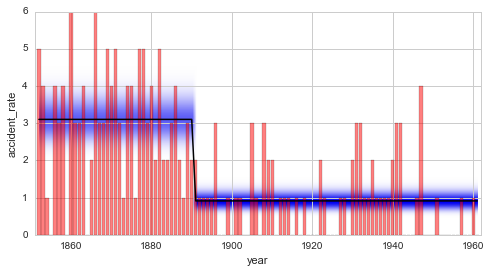
The Bayes factor shows support in favor of the new change-point model. There is a 50% increased probability that the data is generated by the change-point model, compared to the Gaussian random walk model. Some may however argue that the value of \(B = 1.5\) indicates only very weak support and is not worth more than a bare mention. Based on the data at hand, no clear decision between the two models can be made. While the change-point model is favored because it is more restricted (the number of possible data sets that can be described by this model is much smaller than for the Gaussian random walk) and therefore “simpler”, it cannot capture fluctuations of the disaster rate before and after 1890 like the Gaussian random walk model does.
Combined transition models¶
The discussion above shows that depending on the data set, different
transition models better explain different aspects of the data. For some
data sets, a satisfactory transition model may only be found by
combining several simple transition models. bayesloop provides a
transition model class called CombinedTransitionModel that can be
supplied with a sequence of transition models that are subsequently
applied at every time step. Here, we combine the change-point model and
the Gaussian random walk model to check whether the combined model
yields a better explanation of the data, compared to the change-point
model alone:
In [4]:
# combined model (change-point model + Gaussian random walk)
T = bl.tm.CombinedTransitionModel(bl.tm.ChangePoint('tChange', 1890),
bl.tm.GaussianRandomWalk('sigma', 0.2, target='accident_rate'))
S.set(T)
S.fit()
combinedLogEvidence = S.log10Evidence
# determine Bayes factor
B = 10**(combinedLogEvidence - dynamicLogEvidence2)
print '\nBayes factor: B =', B
plt.figure(figsize=(8, 4))
plt.bar(S.rawTimestamps, S.rawData, align='center', facecolor='r', alpha=.5)
S.plot('accident_rate')
plt.xlim([1851, 1962])
plt.xlabel('year');
+ Transition model: Combined transition model. Hyper-Parameter(s): ['tChange', 'sigma']
+ Started new fit:
+ Formatted data.
+ Set prior (function): jeffreys. Values have been re-normalized.
+ Finished forward pass.
+ Log10-evidence: -74.01460
+ Finished backward pass.
+ Computed mean parameter values.
Bayes factor: B = 2.49563205383
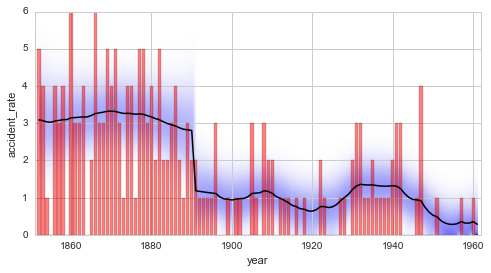
Again, the refined model is favored by a Bayes factor of \(B = 2.5\).
Serial transition model¶
The combined transition models introduced above substantially extend the
number of different transition models. These transition models imply
identical parameter dynamics for all time steps. In many applications,
however, there exist so-called structural breaks when parameter dynamics
exhibit a fundamental change. In contrast to an abrupt change of the
parameter values in case of a change-point, a structural break indicates
an abrupt change of the transition model at a specific point in time.
The class SerialTransitionModel allows to define a sequence of
transition models (including combined transition models) together with a
sequence of time steps that denote the structural breaks. Each
break-point is defined just like any other transition model, containing
a unique name and a time stamp (or an array of possible time stamps, see
this tutorial on change-point studies).
Note, however, that the BreakPoint transition model class can only
be used as a sub-model of an SerialTransitionModel instance.
We use this new class of transition model to explore the idea that the
number of coal mining disasters did not decrease instantaneously, but
instead decreased linearly over the course of a few years. We assume a
static disaster rate until 1885, followed by a deterministic decrease of
0.2 disasters per year (deterministic transition models are defined
easily by custom Python functions, see below) until 1895. Finally, the
disaster rate after the year 1895 is modeled by a Gaussian random walk
of the disaster rate with a standard deviation of \(\sigma=0.1\).
Note that we pass the transition models and the corresponding structural
breaks (time steps) to the SerialTransitionModel in turns. While
this order may increase readability, one can also pass the models first,
followed by the corresponding time steps.
In [5]:
# Definition of a linear decrease transition model.
# The first argument of any determinsitic model must be the time stamp
# and any hyper-parameters of the model are supplied as keyword-arguments.
# The hyper-parameter value(s) is/are supplied as default values.
def linear(t, slope=-0.2):
return slope*t
T = bl.tm.SerialTransitionModel(bl.tm.Static(),
bl.tm.BreakPoint('t_1', 1885),
bl.tm.Deterministic(linear, target='accident_rate'),
bl.tm.BreakPoint('t_2', 1895),
bl.tm.GaussianRandomWalk('sigma', 0.1, target='accident_rate'))
S.set(T)
S.fit()
serialLogEvidence = S.log10Evidence
# determine Bayes factor
B = 10**(serialLogEvidence - combinedLogEvidence)
print '\nBayes factor: B =', B
plt.figure(figsize=(8, 4))
plt.bar(S.rawTimestamps, S.rawData, align='center', facecolor='r', alpha=.5)
S.plot('accident_rate')
plt.xlim([1851, 1962])
plt.xlabel('year');
+ Transition model: Serial transition model. Hyper-Parameter(s): ['slope', 'sigma', 't_1', 't_2']
+ Started new fit:
+ Formatted data.
+ Set prior (function): jeffreys. Values have been re-normalized.
+ Finished forward pass.
+ Log10-evidence: -72.93384
+ Finished backward pass.
+ Computed mean parameter values.
Bayes factor: B = 12.0436384646
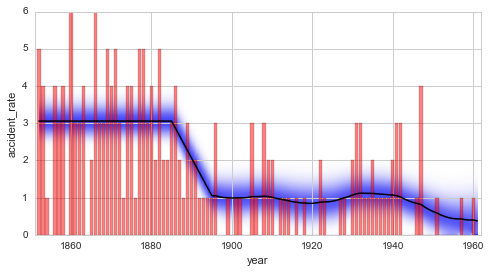
The Bayes factor of the serial model compared to the combined model is determined to \(B = 12.0\). This value indicates positive/strong evidence in favor of the serial model. Keep in mind, though, that the time steps of the structural breaks and the slope of the linear decrease are not inferred in this example, but are instead set by the user. The determined Bayes factor therefore relies on the assumption that these values are true, and the uncertainty tied to these values is therefore not reflected in the value of the Bayes factor. More elaborate studies that take into account the uncertainty tied to these hyper-parameters are introduced here and here.
The iterative approach of creating new hypotheses and comparing them to the best hypothesis currently available provides an objective and never-the-less straight-forward way of exploring new data sets. The subsequent tutorial provides methods to improve upon values for hyper-parameters that are “blindly” set by the user.